在这篇 Fast HotStuff 文章中我们初步引入了 BLS 聚合签名来替代原生 HotStuff 中的阈值签名，本篇文章是 Shardora 在进行 Fast HotStuff 改造过程中对 BLS 聚合签名和门限签名的学习和思考，帮助理清思路。

BLS 签名与特性

BLS 代表 Boneh–Lynn–Shacham，是由斯坦福大学教授Dan Boneh等人于2001年提出的一种签名方案，并在 2018 年进行了更新。BLS 是一个基于椭圆曲线的签名方案，它的特点是基于了双线性映射技术，也就是说，我们可以找到一个很特殊的双线性映射函数 $ e $，传入椭圆曲线上的两个点 $ G_1 $ 和 $ G_2 $ 可以得到一个目标值，即 $ e(G_1,G_2) \to G_t $。

而函数 $ e $ 满足以下特性：

$ e(aG_1,G_2) = e(G_1,aG_2) $

我们可以通过下面的等式完成 BLS 签名的验证：

$ e(S, g_2) = e(HashtoG1(m), pk) $

其中，$ S $ 是签名，$ g_1 $ 和 $ g_2 $ 分别是 $ G_1 $ 和 $ G_2 $ 群的生成元，$ HashtoG1(m) $ 是被签名消息 $ m $ 映射到 $ G_1 $ 上的点，为了方便，后文简写为 $ G1(m) $，$ sk $ 是私钥，$ pk $ 是公钥。

BLS 中，$ S $， $ m $， $ sk $， $ pk $ 有如下关系：

• $ S = G1(m) * sk $
• $ pk = sk * g_2 $

因此可以通过如下推导过程证明上述的验证过程是正确的：

$ e(S, g_2) = e(G1(m)sk, g_2) = e(G1(m), g_2sk) = e(G1(m), pk) $

这段验证逻辑的 C++ 代码如下，注意，由于 BLS 的签名和公钥可以被聚合，下面代码中的 sign 和 pk 无论是聚合前还是聚合后的签名和公钥都是成立的。alt_bn128_ate_reduced_pairing 函数即为上述的双线性映射函数 $ e $， ThresholdUtils::HashtoG1 即为函数 $ G1(m) $。

// 使用公钥对签名进行验证
bool CoreVerify( 
    const libff::alt_bn128_G2& pk, 
    const std::string& message,
    const libff::alt_bn128_G1& sign) {
    // 计算 msg 对应的 G1
    libff::alt_bn128_G1 hash = ThresholdUtils::HashtoG1(message);

    return libff::alt_bn128_ate_reduced_pairing(hash, pk) ==
           libff::alt_bn128_ate_reduced_pairing(sign, libff::alt_bn128_G2::one());
}

BLS 聚合签名方案

签名 $ S $ 就是 $ G_1 $ 群中的一个值，而在 BFT 共识中往往有多个节点同时产生多个签名，这些签名可以通过群加法进行聚合，聚合后的签名和未聚合的签名没有区别，仍是 $ G_1 $ 群中一个值。下面为 BLS 签名的结构体：

struct Signature {
    libff::alt_bn128_G1 sig_;
    // 验签需要对应的参与者公钥，因此必须知道参与者都有谁
    std::unordered_set<uint32_t> participants_;

    inline std::unordered_set<uint32_t> participants() const {
        return participants_;
    }

    inline libff::alt_bn128_G1 signature() const {
        return sig_;
    }

    void set_signature(libff::alt_bn128_G1 g1_sig) {
        sig_ = g1_sig;
    }

    void add_participant(uint32_t member_idx) {
        participants_.insert(member_idx);
    }
}

// 聚合签名和普通签名没有区别
using AggregateSignature = Signature;

BFT 共识中的签名可能是针对同一个消息的，比如 HotStuff 中对同一个视图会产生各自的签名；也可能针对不同的消息，比如 Fast HotStuff 超时视图切换时会对各自的 HighQC 签名。这两种签名都可以进行聚合，也享有相同的验签逻辑，不过针对同一个消息的签名有更快速的验签方法，即使用聚合公钥，下文会进行讲述。

接下来具体学习签名聚合和验签的原理。

签名聚合与普通验签逻辑

我们设网络中有 $ t $ 个节点，分别针对 $ m_1,m_2,…,m_t $ 进行签名，生成 $ S_1,S_2,…,S_t $。我们可以将这些签名聚合按照如下方式聚合：

$ S_{agg} = S_1 + S_2 + … + S_t $

代码如下，聚合时要同时记录签名者的身份，用于找到对应的公钥进行验证。

Status AggregateSigs(
        const std::vector<Signature*>& sigs,
        AggregateSignature* agg_sig) {
    libff::alt_bn128_G1 agg_g1;
    
    for (const auto sig : sigs) {
        // 聚合这些签名
        agg_g1 = agg_g1 + sig->signature();
        // 记录签名者信息
        for (const uint32_t member_id : sig->participants()) {
            agg_sig->add_participant(member_id);
        }
    }

    agg_sig->set_signature(*agg_g1_sig);
    return Status::kSuccess;
}

我们对于聚合后的签名 $ S_{agg} $ 的验证逻辑为：

$ e(S_{agg}, g_2) = e(G1(m_1), pk_1)e(G1(m_2), pk_2)…e(G1(m_t), pk_t) $

推导过程如下：

$ e(S_{agg}, g_2) = e(S_1 + S_2+… + S_t, g_2) $

$ =e(S_1,g_2)e(S_2,g_2)…e(S_t,g_2) $

$ = e(G1(m_1)sk_1,g_2)e(G1(m_2)sk_2,g2)…e(G1(m_t)sk_t, g_2) $

$ = e(G1(m_1), sk_1g_2)e(G1(m_2), sk_2g_2)…e(G1(m_t), sk_tg_2) $

$ = e(G1(m_1), pk_1)e(G1(m_2), pk_2)…e(G1(m_t), pk_t) $

不难看出，这里的计算量随着聚合签名数量的增大而增大的，这是因为被签名的消息是不同的，没有办法再做优化。Fast HotStuff 的 Unhappy Path 视图切换时就会遇到这种场景，每个节点需要对各自的 HighQC 进行签名，这个 HighQC 可能是不同的，而新 Leader 在验证聚合签名时就需要用到这种验签方式。

以下是项目代码中的实现方式：

bool AggregatedVerify(
        std::vector<std::string> str_hashes,
        const libff::alt_bn128_G1& agg_sig,
        const std::vector<libff::alt_bn128_G2> pks ) {
    // 消息数量和公钥数量必须相同
    if (str_hashes.size() != pks.size()) {
        return false;
    }

    // 等式右侧
    auto right = libff::alt_bn128_GT::one();
    for (uint32_t i = 0; i < pks.size(); i++) {
        auto hash_g1 = libBLS::ThresholdUtils::HashtoG1(str_hashes[i]);
        // 不同映射函数结果相乘
        right = right * libff::alt_bn128_ate_reduced_pairing(hash_g1, pks[i]); 
    }

    // e(S, g2) = e(G1(m1), pk1)...e(Gt(mt), pkt)
    return libff::alt_bn128_ate_reduced_pairing(agg_sig, libff::alt_bn128_G2::one()) == right;
}

密钥聚合与快速验签逻辑

如果不同节点对同一个消息 $ m $ 做签名并进行聚合，那么对聚合签名的验证逻辑就可以得到优化，即使用聚合公钥进行验签，推导如下：

$ e(S_{agg}, g_2) = e(S_1 + S_2+… + S_t, g_2) $

$ = e(G1(m), pk_1)e(G1(m), pk_2)…e(G1(m), pk_t) $

$ = e(G1(m), pk_1+pk_2+…+pk_t) $

$ = e(G1(m), pk_{agg}) $

使用聚合后的公钥 $ pk_{agg} $ 对聚合后的签名 $ S_{agg} $ 进行验证，验证逻辑与普通公钥对普通签名的验证逻辑一致。代码如下：

bool FastAggregateVerify(
        const std::vector<libff::alt_bn128_G2>& pks, // 各节点公钥
        const std::string& str_hash, // 对相同消息签名
        const libff::alt_bn128_G1& agg_sig) {
    // 聚合公钥
    libff::alt_bn128_G2 agg_pk =
        std::accumulate( pks.begin(), pks.end(), libff::alt_bn128_G2::zero() );

    // 使用聚合后的公钥对聚合后的签名做常规验证
    return CoreVerify(agg_pk, str_hash, agg_sig);
}

POP 与密钥消除攻击

在 BLS 签名库中可以看到有两个函数，PopProve 和 PopVerify，其中的 Pop 是 Proof of Posession 的缩写，意为拥有对应私钥的凭证，来看代码。

// 使用对公钥哈希值的签名作为 proof，证明自己确实持有对应的私钥 sk
libff::alt_bn128_G1 PopProve(const libff::alt_bn128_Fr& sk) {
    libff::alt_bn128_G2 pk = sk * libff::alt_bn128_G2::one();
    // 对公钥进行签名
    libff::alt_bn128_G1 hash = HashPublicKeyToG1(pk);
    libff::alt_bn128_G1 ret = sk * hash;

    return ret;
}

// 验证 proof，proof 即为对 pk 的签名
bool PopVerify(const libff::alt_bn128_G2& pk, const libff::alt_bn128_G1& proof ) {
    libff::alt_bn128_G1 hash = HashPublicKeyToG1(pk);

    // e(G1(m), pk) = e(S, g2)
    return libff::alt_bn128_ate_reduced_pairing(hash, pk) ==
           libff::alt_bn128_ate_reduced_pairing(proof, libff::alt_bn128_G2::one());
}

PopProve 函数是对自己的公钥做签名，而 PopVerify 是对该签名进行验证。

对 $ pk $ 进行签名生成的 $ proof $ 可以用于证明该参与者确实拥有该 $ pk $ 对应的 $ sk $，否则该 $ proof $ 无法被 $ pk $ 验签通过。而之所以要证明节点拥有 $ pk $ 对应的私钥是为了防范聚合签名下的「密钥消除攻击」。

假设系统存在 $ A $， $ B $ 两个节点，对同一个消息进行聚合签名如下，

$ S_{agg}=S_A+S_B=G1(m)sk_A+G1(m)sk_B $

正常来说聚合后的签名将可以通过两个节点聚合后的公钥 $ pk_{agg} = pk_A + pk_B $ 进行验证，然而 $ B $ 是一个恶意节点，提供了一个虚假的公钥 $ pk_{B’} $，且满足 $ pk_{B’}=pk_B-pk_A $，那么聚合后公钥就变成了 $ pk_{B} $ 自己。

$ pk_{agg} = pk_A + pk_{B’}=pk_A+(pk_B-pk_A)=pk_B $

这意味着 $ B $ 自己一个人就可以制造出聚合后的签名 $ S_{agg} $。这种攻击称为密钥消除攻击（属 Rogue Key Attacks）。解决方案有两个，

第一，使用他人的公钥 $ pk $ 之前，需要对该节点提供的 $ proof $ 做验证，确保该公钥确实是该节点使用自己的私钥产生的。

第二，对签名和公钥进行聚合时，不是简单的相加，而是加入非线性系数，如下：

$ S_{agg}=a_1S_1+a_2S_2+…+a_tS_t $

$ pk_{agg}=a_1pk_1+a_2pk_2+…+a_tpk_t $

这个系数可以通过所有参与者的公钥共同得出，如将签名者的公钥与所有节点的公钥进行拼接：

$ a_i=Hash(pk_i || pk_1||pk_2||…||pk_t) $

Pop 往往用在公钥分发阶段，在 HotStuff 项目中，每个 epoch 开始前节点之间需要共享各自公钥 $ pk $，那么同时也需要发送该公钥对应的 $ proof $ （PopProve 产生），在收到其他节点的 $ pk $ 和 $ proof $ 后需要使用 PopVerify 进行验证，通过后该公钥才能用于后续的验签。

BLS 阈值签名方案

原生的 HotStuff 论文使用了阈值签名的方案，BLS 阈值签名是一个 t-n 签名，即收集到 t 个签名之后即可通过验证。阈值签名的底层原理是基于多项式的秘密分享协议，在实际工程中我们使用 VSS（可验证秘密分享协议）与 CSS（完整秘密分享协议）更多，以保证工程上可靠性和安全性。

秘密分享（SS）

秘密分享是将一个秘密 $ s $ 分享给多个参与者，并且可以通过这些参与者所拿到的秘密份额进行恢复。最朴素的想法当然是异或，然而异或无法实现 t-n 的门限性质，这是阈值签名的基本要求。

因此我们使用 Shamir 秘密分享方案，它的原理是利用一个 t 阶的多项式隐藏秘密 $ s $，如下:

$ f(x)=s+a_1x+a_2x^2+…+a_tx^t $

这样我们可以将 $ f(x) $ 的值作为秘密的份额发送给全部 n 个节点，即 $ f(1),f(2),…,f(n) $，然后只需要任意 $ t $ 个秘密份额就可以通过拉格朗日插值法恢复出秘密 $ s $（无需恢复完整的多项式）。

可验证秘密分享（VSS）

收到一份他人分享的秘密份额时，我们无法验证该份额的真实性，这时候就需要多项式承诺。多项式承诺作为一个证明，需要在分发秘密份额时一同发送给接收方。比如多项式为：

$ f(x)=s+a_1x+a_2x^2+…+a_nx^n $

其中 $ s $ 为节点要分享的秘密，那么要分享给 $ i $ 的秘密份额称为 $ s_i $。我们定义多项式承诺为 $ C_f=[c_1,c_2,…c_n] $

其中 $ c_i $ 的计算方式为：

$ c_i=g^{a_i}\ mod\ p $

这是一个离散对数的计算，因此即使知道 $ c_i $ 也无法还原 $ a_i $。当节点 $ i $ 收到 $ s_i $ 和 $ c_i $ 后就可以通过下面公式进行验证。

$ g^{s_i}=\prod^{k-1}_{j=0}(c_j)^{i^j}\ mod\ p $

同理，椭圆曲线多项式承诺计算方法为：

$ c_i=a_ig $

验证方法为：

$ s^i⋅g=c_0+ic_1+i^2c_2+⋯+i^ic_t $

工程项目中，往往会在第一轮将多项式承诺 $ C_f $ 进行广播，然后在第二轮接受秘密时进行验证。

分布式密钥生成（DKG）

门限签名实际上是个单签名，使用一个虚拟的私钥签名并使用其对应的公钥验签，而每个节点持有的仅是该虚拟私钥的一部分份额，使用该私钥份额生成的部分签名最终可以恢复出完整的签名，私钥份额也对应于一个完整的虚拟私钥，如下图。

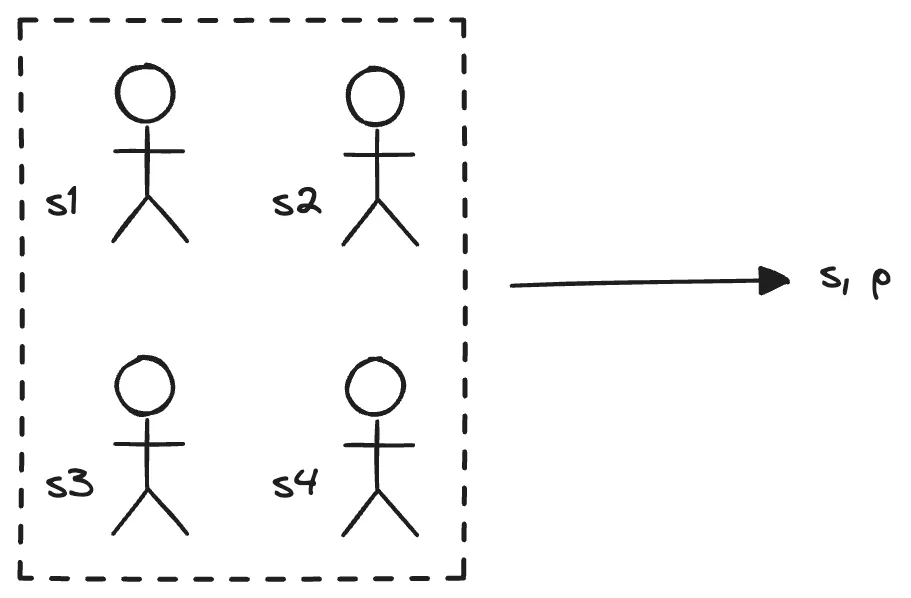
图中，私钥 $ s $ 是一个虚拟的私钥，由于分布式系统中没有可信中心，因此没有节点真正拥有这个私钥，这个私钥是通过秘密分享的方式分发给所有 $ n $ 个节点的。多项式如下：

$ f(x)=s+a_1x+a_2x^2+…+a_nx^n(virtual) $

当然由于没有节点有权利拥有真实的私钥 $ s $，这个多项式也是虚拟的，实际工程中我们并看不到这个多项式，所以所谓的 DKG 就是解决如何在没有这个多项式的前提下如何将 **$ s $ 的份额分发给所有节点**。

我们假设节点 $ k $ 最后拥有的私钥份额为 $ s_k $，那么在分布式条件下，每个人的私钥份额 $ s_k $ 必须包含随机性，不能被恶意的决定。如果最多存在 $ f $ 个恶意节点，那么 $ s_k $ 需要有 $ f+1 $ 个节点贡献的随机值共同组成。

我们定义每个节点拥有一个随机值秘密，定义为 $ z $， $ z_{k} $ 就表示节点 $ k $ 拥有的随机值秘密，这个秘密可以通过各节点自己的多项式进行分享，如下：

$ g_k(x)=z_k+a_{k1}x+a_{k2}x^2+…+a_{kn}x^n $

定义 $ z_{kn} $ 为 $ z_k $ 发给节点 $ n $ 的分量，即 $ g_k(n) $。那么节点 $ k $ 的私钥份额就可以被每个节点的随机值分量一同贡献出来，从而保证随机性，只要保证 $ z_k $ 和 $ s_k $ 是同一个循环群中的，就可以定义以下关系 ：

$ s_k = g_k(1)+g_k(2)+…+g_k(n) = z_{1k} + z_{2k}+…+z_{nk} $。

在实际项目中， $ z_k $ 是 BLS 签名生成的一个私钥，只不过这里充当了提供随机值的待分享的秘密，$ t $ 个节点的 $ z $ 分量可以组成一个私钥份额 $ s_{k} $。

在实际工程中，DKG 往往拥有两个轮次的消息传播。第一轮，各节点生成各自多项式承诺 $ C_f $ 并广播给其他节点，各节点存储其他节点发送而来的多项式承诺；第二轮，各节点两两交换密钥份额 $ z $，收到对应份额时使用多项式承诺进行验证，当收集达到 $ t $ 个后构建出虚拟私钥的份额 $ s_{k} $。下面是 Shardora 的 DKG 代码：

// 定时任务
void BlsDkg::TimerMessage() {
    if (!has_broadcast_verify_) {
        // 广播多项式承诺
        BroadcastCommitment();
        has_broadcast_verify_ = true;
    }

    if (has_broadcast_verify_ && !has_broadcast_swapkey_) {
        // 两两分享私钥 z
        SwapSecKey();
        has_broadcast_swapkey_ = true;
    }

    if (has_broadcast_swapkey_ && !has_finished_) {
        // 生成最终的虚拟私钥份额
        Finish();
        has_finished_ = true;
    }
}

HotStuff 需要的是 t-n 签名吗？

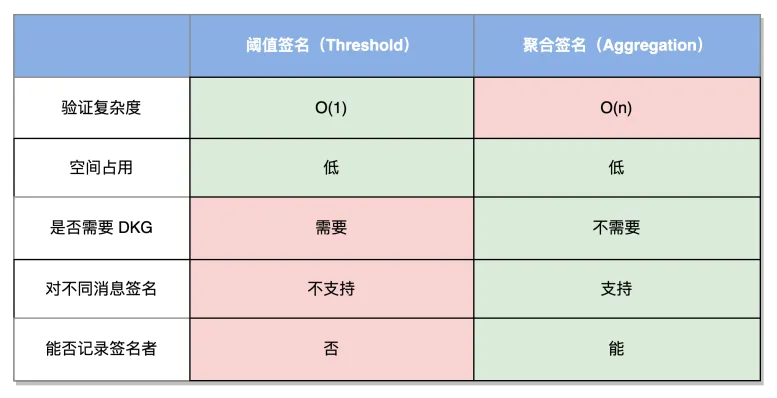
HotStuff 或者其他 BFT 类共识算法对于投票的收集有一个 t-n 的逻辑，即只要收集到 +2/3 的同意投票就生成群体证明（QC），这让人天然的觉得我们需要一个 t-n 的签名方案，即阈值签名。而聚合签名是将 n 个签名进行聚合，并一起进行验证，从而达到节省空间，节省计算时间的目的，因此是一个 n-n 的签名方案。这就很容易造成疑问和误解，HotStuff 一定需要一个 t-n 的签名方案吗，n-n 的聚合签名是不是无法满足？比较聚合签名和阈值签名的特性：

• 聚合签名：只是把多个签名整合在一起，一起进行传输和验证，与签名的数量无关。
• 门限签名：只有当收集到 t 数量的签名份额后，门限签名才能通过验证，与数量相关。

不妨再想 HotStuff 的签名验签场景：收集到固定（2/3+1）数量（或权重）的投票并进行验证。这其中包含两个验证项：

• 所有签名必须合法。
• 签名的数量必须 > 2/3。

签名的合法性是任何签名方案的基础因此不必多说，阈值签名是天然包含对签名数量的验证逻辑的（这部分信息在 DKG 时就已经嵌入），然而，我们完全可以单独写代码判断一下收集到的签名数量是否达到要求，从而改用聚合签名。

因此从功能上来说，BFT 共识没有必要使用阈值签名，甚至只使用普通的签名方案逐一进行签名验签就可以实现，我们使用阈值签名只是为了优化签名占用的空间以及验证签名需要的计算量，并不是功能上的考量。

其实，Shardora 在实际开发阈值签名方案后就遇到了以下问题：

• 每个 epoch 由于需要对共识委员会中的节点重新配置，需要重新进行 DKG 以分发虚拟私钥份额，这需要几分钟的时间，这使得某一 epoch 的共识委员会选出后不能立刻参与共识，而是要再下下轮生效。
• DKG 大大增加了代码复杂度。
• 阈值签名不带有签名者的身份信息，因为任意 $ t $ 个份额都可以重建签名，我们也就无法对签名者进行激励。
• 无法对接 PoS，阈值签名的门限值只能是节点的数量，不能使用别的权重信息。

后改用聚合签名就完美的解决了这些问题。

• 聚合签名可以知道并验证投票者的身份，从而分发奖励。
• 聚合签名的数量是单独验证的，因此可以使用 Stake 作为阈值。
• 删掉了复杂的 DKG 逻辑。
• 使得实现 Fast HotStuff 方案成为可能。

最后附上聚合签名和阈值签名的对比。

推荐阅读

• MuSig2：Schnorr 的多签名
• 密钥消除攻击
• 区块链中的数学 - Feldman的可验证的密钥分享
• 【密码学（2）】-BLS聚合签名
• libbls 代码
• DKG 代码